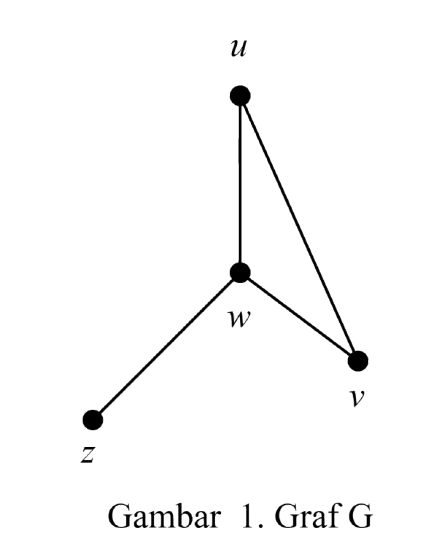
Ditunjukkan pada gambar 1 terdapat graf G sederhana yang himpunan simpulnya \( V(G) \) adalah \( {u, v, w, z}, \) dan himpunan sisinya \( E(G) \) terdiri dari sisi-sisi \( uv, uw, vw \) dan \( wz. \) Istilah dan simbol tersebut merupakan definisi-definisi yang digunakan untuk graf.
Dimensi Metrik
Konsep dimensi metrik pertama kali diperkenalkan oleh Harary dan Melter pada tahun 1966. Himpunan simpul \( W \) dalam graf \( G \) disebut sebagai himpunan pembeda (resolving set) apabila setiap simpul dapat dibedakan berdasarkan jaraknya ke simpul-simpul dalam \( W \), sedangkan dimensi metrik dari graf \( G \) adalah jumlah paling sedikit simpul dalam himpunan tersebut.
Definisi (Chartranda et al., 2000)
Setiap simpul v dalam Graf G direpresentasikan dengan sebuah vektor jarak yang menunjukkan jarak simpul tersebut ke setiap simpul dalam W yaitu: \[ r(v \mid W) = (d(v, w_1), d(v, w_2), \ldots, d(v, w_k)) \]
Definisi (Slamin, 2023)
Himpunan \( W \) dikatakan sebagai himpunan metrik lokal apabila setiap pasangan simpul yang bertetangga memiliki representasi jarak yang berbeda terhadap \(W,\) maka \( r(u \mid W) \ne r(v \mid W), \) dan dimensi metrik lokal dari graf \( G \) dinotasikan dengan \( \text{dim}_{l}(G) \).
Teorema (Slamin, 2023)
Jika \( \text{dim}_{l}(G) = n-1 \) jika dan hanya jika \( G \) adalah graf Lengkap \( \text{K}_{n} \), dan \( \text{dim}_{l}(G)=1 \) jika dan hanya jika \( G \) adalah garf dua partisi \( \text{K}_{m,n} \).
Definisi (Brigham et all., 2003)
Suatu himpuna \( S \) dikatakan sebagai himpunan pembeda dominasi (dominating resolving set) jika memiliki dua fungsi sekaligus yaitu sebagai himpunan pembeda (resolving set) dan himpunan dominasi (dominating set).
Definisi (Slamin, 2023)
Suatu himpunan pembeda dominasi dengan jumlan kardinalitas minimum disebut basis dominasi. Banyaknya titik (vertex) dalam basis dominasi dari graf \( G \) disebut sebagai dimensi metrik dominasi yang dilambangkan sebagai \( Ddim(G). \)
Dimensi Metrik Lokal Dominasi
Teori dimensi metrik lokal dominasi merupakan pengembangan baru dalam teori graf yang mengombinasikan dua konsep sebelumnya, yaitu dimensi metrik lokal dan himpunan dominasi (dominating set). Dengan menggabungkan kedua konsep ini, dimensi metrik lokal dominasi tidak hanya memastikan setiap titik dapat direpresentasikan secara berbeda berdasarkan jaraknya terhadap himpunan tertentu, tetapi juga menjamin bahwa himpunan tersebut mendominasi seluruh graf.
Untuk graf terhubung \( G \), suatu himpunan terurut \( \ W_{l} = \{ w_1, w_2, \ldots, w_n \} \subseteq V(G)\) disebut himpunan pembeda lokal dominasi jika memenuhi dua syarat, yaitu himpunan pembeda lokal sekaligus himpunan dominasi dalam graf \( G \).
Definisi 1
(Umilasari et al., 2021)
\( \text{Ddim}_{l}(G)=1 \) jika dan hanya jika \( \ G ≡ {S}_{n}, n ≥ 3. \)
Teorema
(Umilasari et al., 2024)
Jika himpunan tersebut memiliki jumlah kardinalitas paling sedikit, maka disebut basis lokal dominasi. Banyaknya elemen dalam basis lokal dominasi disebut dimensi metrik lokal dominasi dari graf \( G \), yang dinotasikan sebagai \( \text{Ddim}_{l}(G) \).
Definisi 1
(Umilasari et al., 2021)
Definisi 1 (Umilasari et al., 2021).
Untuk graf terhubung \( G \), suatu himpunan terurut \( \ W_{l} = \{ w_1, w_2, \ldots, w_n \} \subseteq V(G)\) disebut himpunan pembeda lokal dominasi jika memenuhi dua syarat, yaitu himpunan pembeda lokal sekaligus himpunan dominasi dalam graf \( G \).
Teorema (Umilasari et al., 2024).
\( \text{Ddim}_{l}(G)=1 \) jika dan hanya jika \( \ G ≡ {S}_{n}, n ≥ 3. \)
Definisi 2 (Umilasari et al., 2021).
Jika himpunan tersebut memiliki jumlah kardinalitas paling sedikit, maka disebut basis lokal dominasi. Banyaknya elemen dalam basis lokal dominasi disebut dimensi metrik lokal dominasi dari graf \( G \), yang dinotasikan sebagai \( \text{Ddim}_{l}(G) \).